[This is a long, perhaps tedious, post with many variations of a program that finds the timing of Arduino loops and operations. The punchline is that in 1 second my system can do about 86,000 floating point (multiplication) operations, or about 700,000 integer (multiplication) operations. Division takes 3 (float) to 10 (int) times longer. All the rest is detail.]
I'd like to implement a simple active visual system using the photoresistor and LED's on the Android ADK shield (see "Does not compute...") controlled by a program implemented on the Arduino Mega 2560 microcontroller. This requires flashing the LED's, and they are bright enough that it is pretty darned irritating if the flashing is visible.
But if they flash fast enough we don't perceive it as flashing, just a bright light. Above the flicker fusion threshold of about 15 Hz a flashing light appears as a steady light. Movies and video have a 25 to 30 Hz frame rate to avoid flicker. There's a reason that 'flick' is shorthand for moving picture.
How much processing can be done in one cycle through the program loop on an Arduino if the time permitted is less than about 1/20 second = 50 ms (milliseconds)?
To get a feel for this, I could use a program with a loop containing one or several operations, to see how fast that runs. But without an oscilloscope I don't have a chance at measuring the frequency of the loop execution. Even with an oscilloscope it would not be clear which periodic signal corresponds to the loop frequency.
So I want to use the program itself to measure the timing of loop execution. To do this, it is convenient to write text to the serial monitor (see appendix for full code listings). This loop function gets and writes the time since the program started, in milliseconds:
void loop(){
// Every time through the loop write time since starting to
// the serial monitor.
Serial.println( millis() );
}
with the serial monitor output:
Each line corresponds to one pass through the loop, and there is a consistent 6 ms time difference between each of them. That's a good chunk of 50 ms, and worth worrying about.
This millisecond temporal resolution is good for a rough estimate, but we can do better with the microsecond (one millionth of a second) reporting function micros() instead of millis(). The corresponding output is:
The differences are still consistent, but the differences are larger:
9360 microseconds = 9.36 ms
It might be that the micros() function takes longer to execute than millis(), and/or it takes longer to send and print out seven digits than it does four. I measured the time needed to execute these time functions (see appendix), and while they are different (1.3 and 3.3 microseconds, respectively) they are small compared with the serial send and print operations.
The ratios of a loop times to number of digits are similar, within the precision of the 6 ms measurement:
6/4 = 1.50 ms/character
9.36/7 = 1.34 ms/character
To test if the number of characters in the serial output is slowing things down (and by the way, serial means one bit at a time through a
serial port), this loop has another serial write with a longer string:
void loop(){
// At every loop cycle write time to the serial monitor.
Serial.print( micros() );
Serial.println( " microseconds up to this loop" );
}
with output:
Now the sequential differences are about 39500 microseconds = 39.5 ms, and the time per character is:
39.5/36 = 1.1 ms/character
In any case, about 1 ms is ne
eded for sending each character to the serial port. Note that the serial communication rate was set to 9600 baud (lower right corner). This means that an 8-bit character, assuming the
bit rate the is about the baud rate, was sent in about:
(1000 ms/s)*(8 bits/character)/ (9600 bits/s) = .833 ms
and the rest of the time taken for the loop is due to executing the function calls.
Setting the serial rate to the maximum, 115200 baud results in a faster loop:
Now it only takes about 3780 microseconds = 3.78 ms to send the 36 characters, more than 10 times as fast.
At this rate the loop frequency is:
(1000 ms/s) / (3.78 ms/loop) = 264 Hz (loop cycles/second)
I wonder if it can write faster if the serial monitor is not displayed? Perhaps the serial monitor needs to display a character or line before it will accept the next character or line of characters. At this baud rate the display update is jerky, displaying several lines with pauses in between. I don't know exactly why.
For estimating the speed of various operations I want to average loop time differences over many loops, and ignore the time it takes for the time and text output functions. This code
increments a
counter (
++nLoopCounter) each time through the loop, compares the count with a large number, and then reports information about the average time for a loop. Note that the time it takes for averaging and sending text to the serial monitor is not included in the reported timing:
int nLoopCount = 0;
int nLoopsReport = 32000;
int tLast = 0;
int tDelta = 0;
float flLoopRate = 0;
void loop(){
// Don't do anything here, but this is where some
// operations would go.
// ...
// Every nLoopsReport times through the loop,
// write stats to the serial monitor.
++nLoopCount;
if ( nLoopCount == nLoopsReport ) {
tDelta = millis() - tLast;
Serial.print( tDelta );
Serial.print( " milliseconds per " );
Serial.print( nLoopsReport );
Serial.println( " loops" );
flLoopRate = (1000.0*nLoopsReport)/tDelta;
Serial.print( flLoopRate, 0 );
Serial.println( " loops/s (Hz)" );
nLoopCount = 0;
tLast = millis();
}
}
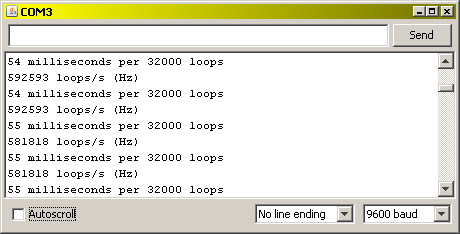
The serial monitor output looks like:
Now we're talking fast; half a million loops per second, or 500 KHz = .5 MHz! Compare this with how long it took to do the serial calls a rate only about 264 loops/s -- about 2000 times slower.
Exactly what operations were done during one loop, that took 2 microseconds to complete?
execute the loop
increment the counter
compare the counter with a variable
The clock rate is 16 MHz, so it appears that about 32 clock tics are needed to carry out these operations.
None of these short steps can be avoided, but can they be shortened? Yes.
Note that the somewhat arbitrary value 32000 was used for the number of loops to average. This could have been less (say 10000), but it could not be much more. The Arduino is a 16-bit machine (the CPU operates on 16-bit chunks of data), and the type int is sized accordingly. A signed 16-bit integer,
int, has the range [-32,768, 32,767] = [-2^15, (2^15) - 1].
More loops could be averaged if the
unsigned int type was used (up to 64,000), or the
long or
unsigned long type (up to 2,000,000,000 or 4,000,000,00 respectively). But if a longer integer type is used (for both the counter and the number of loops to average), the increment and compare function calls take longer, resulting in about 20% loss of speed, at 408 KHz.
There is an option for using a shorter integer type,
byte or the equivalent
unsigned char. But these unsigned types have a range of only [0,255]. It is marginally faster:
It loops at about 750 KHz = .75 MHz, corresponding to about 1.3 microsecond/loop. That's as fast as I could execute a loop that periodically reports timing.
Now I can add math functions to the loop:
// Do some math, see how much longer it takes:
An average of 86.4 KHz for the whole loop! More time is spent on this floating point operation (
FLOP) than the loop/increment/compare used for reporting these statistics. The time for the loop/increment/compare is 1.33 microseconds (from above), and so the floating point operation takes about:
t(FLOP) = ( 2940 microseconds / 255 loops ) - 1.33microseconds ~= 10.2 microseconds
You might think that a CPU can anticipate that every time through the loop the same numbers (flFLOPvalue1 and 1.0001) are needed, and so the CPU will not have to retrieve the number from memory by keeping it in the register. It is true that modern compilers can sometimes produce optimized machine code that recognizes these regularities, and a
CPU cache can reduce the need to go to memory. I don't know what optimizations occur in this case, or if they occur at all.
But the compound multiplication operation *= can use a shortcut because only one register is needed for one of the arguments (
flFLOPvalue1) and the result. A more general FLOP requires three registers, the two arguments and a result, like flA = flB*flC. Trying this out results in an almost identical result so it appears that this optimization is not used or doesn't result in a speed increase.
So this answers my basic question, how many (multiplication) operations can be performed in 1/20th of a second:
(1 s/20) * 86,400 float operations / s ~= 4300 FLOP in 1/20 second
The corresponding result for the integer operation, multiplication, is:
(1 s/20) * 700,000 float operations / s ~= 35000 INTOP in 1/20 second
There is a huge performance hit for division and some other operations (see list in appendix). Floating point division takes about three times as long as floating point multiplication, and integer division takes about 10 times as long as integer multiplication.
That's a generous number of operations available in the blink of an eye. I think a robot with good visual comprehension is possible with the right programming, and efficient use of these operations. If the computational capacity is not exhausted using one eye spot (a photoresistor), then maybe several eyespots can be accomodated.
Appendix:
Here's a short list of the time it takes to do particular operations, including integer operations. See operation_time_1 program below, which was used to find these values.
Floating point (float) result:
addition of two floating point numbers, assignment to a third:
10.3 microseconds, or 97 K operations/s
multiplication (*) of two floating point numbers, assignment to a third:
10.3 microseconds, or 97 K operations/s
compound multiplication (*=) of floating point numbers:
10.4 microseconds, or 96 K operations/s
compound multiplication (*=) of float with an explicit float
10.2 microseconds, or 98 K operations/s
division (/) of two floating point numbers, assignment to a third:
32.7 microseconds, or 30.5 K operations/s
addition of 16-bit integers:
.88 microseconds, or 1,100 K operations/s
multiplication of 16-bit integers (int):
1.43 microseconds, or 700 K operations/s
division of 16-bit integers (and truncation to int):
15.7 microseconds, or 63.6 K operations/s
division of 16-bit integer by float (and truncation to int):
43.1 microseconds, or 23.2 K operations/s
addition of 16-bit integer and a float (and truncation to int):
20.6 microseconds, or 48.5 K operations/s
modulo (2) operation on 16-bit integer;
15.7 microseconds, or 63.8 K operations/s
Floating point math operations:
trigonometric floating point operation, cos()
113 microseconds, or 8.9 K operations/s
irrational math floating point operation, sqrt()
47 microseconds, or 21 K operations/s
Utilities:
111 microseconds, or 9.0 K operations/s
From the function reference:
"It takes about 100 microseconds (0.0001 s) to read an analog input, so the maximum reading rate is about 10,000 times a second."
6.7 microseconds, or 150 K operations/s
n microseconds, to within the precision of the reporting time estimate
millis();
1.7 microseconds, or 590 K operations/s
micros();
3.3 microseconds, or 300 K operations/s
To Do: comparison, casting (conversion) operations, more math, control structures
To Do: byte, double (no, same size as float) and long operations
This program was used for calculating the statistics for single operations:
//
// operation_time_1
//
// Estimate operation(s) time on an Arduino CPU.
// Average the time needed for an operation, or set of operations,
// over 255 loop cycles, and report statistics.
//
// USAGE:
//
// Find and hardcode loop time with no operations. Then add
// an operation and run again.
//
// HARDCODED:
//
// The operations to be timed.
//
// flTReport: // Time required for reporting alone.
// // Find by running this program with no function calls
// // before the counter (and ignore stats that depend on
// // this value).
//
// created by Mark Dow, June 24, 2011
// modified by Mark Dow, June 26, 2011 (better reporting)
//
////////////
// harcoded:
flTReport = 1.333; // Time required for reporting alone.
// Find by running this program with no function calls
// // before the counter (and ignore stats that depend on
//////////// // this value).
#define LED_2_BLUE 6
#define PHOTORESISTOR A2
byte nLoopCount = 0;
const byte nLoopsReport = 255;
int tLast = 0;
int tDelta = 0;
float flLoopRate = 0;
// Arbitrary operation variables:
float flFLOPvalue1 = 1.00001;
float flFLOPvalue2 = 1.00002;
float flFLOPvalue3 = 1.00003;
int nINTOPvalue1 = 2;
int nINTOPvalue2 = 3;
int nINTOPvalue3 = 5;
void setup(){
Serial.begin( 9600 );
pinMode( LED_2_BLUE, OUTPUT );
pinMode( PHOTORESISTOR, INPUT );
}
void loop(){
// Do some math, or any operation, to see how much longer it
// takes than reporting alone.
flFLOPvalue1 = flFLOPvalue2 * flFLOPvalue3;
// flFLOPvalue1 = flFLOPvalue2 * flFLOPvalue3;
// flFLOPvalue1 *= flFLOPvalue2;
// flFLOPvalue1 *= 1.0001;
// flFLOPvalue1 = flFLOPvalue2 / flFLOPvalue3;
// nINTOPvalue1 = nINTOPvalue2 + nINTOPvalue3;
// nINTOPvalue1 = nINTOPvalue2 * nINTOPvalue3;
// nINTOPvalue1 = nINTOPvalue2 / nINTOPvalue3;
// nINTOPvalue1 = nINTOPvalue2 / flFLOPvalue1;
// nINTOPvalue1 = nINTOPvalue2 * flFLOPvalue1;
// nINTOPvalue1 = nINTOPvalue2 % 2;
// flFLOPvalue1 = cos( flFLOPvalue2 );
// flFLOPvalue1 = sqrt( flFLOPvalue2 );
// analogRead( PHOTORESISTOR ); // analog read
// digitalWrite( LED_2_BLUE, HIGH ); // digital write
// delayMicroseconds( 50 );
// nINTOPvalue1 = millis();
// nINTOPvalue1 = micros();
// Every nLoopsReport times through the loop, write stats to the serial
//monitor.
++nLoopCount;
if ( nLoopCount == nLoopsReport ) {
tDelta = micros() - tLast;
Serial.print( tDelta );
Serial.println( " microseconds per 255 loops" );
flLoopRate = (1000000.0*nLoopsReport)/tDelta;
Serial.print( flLoopRate, 0 );
Serial.println( " loops/s (Hz)" );
Serial.println( "Operation(s) without stats: " );
// Subtract off time without any operations (this loop),
// about 1.333 microseconds on Arduino Mega 2560.
Serial.print( ( float(tDelta)/nLoopsReport ) - 1.333 );
Serial.print( " microseconds, or " );
Serial.print( 1000/(( float(tDelta)/nLoopsReport ) - 1.333) );
Serial.println( " K operation(s)/s" );
Serial.println( "" );
nLoopCount = 0;
tLast = micros();
}
}
This program and variations of it was used for calculating finding statistics of loop that only report loop time:
//
// loop_timer_5
//
// Estimate loop time on the Arduino Mega 2560.
// Print to serial port the time required for many loops,
// each containing one increment and one control structure
// comparison.
//
//
// created by Mark Dow, June 23, 2011
//
unsigned long nLoopCount = 0;
//const byte nLoopsReport = 255;
//const int nLoopsReport = 32000;
//const unsigned int nLoopsReport = 64000;
const unsigned long nLoopsReport = 1000000;
int tLast = 0;
int tDelta = 0;
float flLoopRate = 0;
void setup(){
Serial.begin( 9600 );
}
void loop(){
// Don't do anything here, but this is where some operations would go.
// ...
// Every nLoopsReport times through the loop, write stats to the serial
//monitor.
++nLoopCount;
if ( nLoopCount == nLoopsReport ) {
tDelta = millis() - tLast;
// tDelta = micros() - tLast;
Serial.print( tDelta );
Serial.print( " milliseconds per " );
Serial.print( nLoopsReport );
Serial.println( " loops" );
flLoopRate = (1000.0*nLoopsReport)/tDelta;
Serial.print( flLoopRate, 0 );
Serial.println( " loops/s (Hz)" );
nLoopCount = 0;
tLast = millis();
// tLast = micros();
}
}