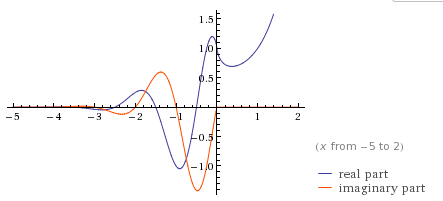
Secnarf got me interested in the function x^x, which is real valued for positive values of x, but wonderfully complex for negative x.
Functions that are powers of a variable are often more simple after taking a logarithm of the function, so I was curious what ln(x^x) might look like:
Sure enough, the imaginary part of this function is piecewise linear. What are the slopes of these segments? For that we just need the derivative with respect to x, d( ln( x^x) )/dy (function in blue, derivative in magenta):
The imaginary part of the derivative (bottom, magenta), shows that the slope is constant, a bit more than 3. In fact, the slope is exactly half tau.
Something similar happens (for the same reason) when we take the logarithm of both sides of Euler's identity:
ln( e^i*τ/2 ) = ln( -1 )
which can be used as defining the logarithm of a negative number. This reduces to:
i * τ/2 = ln( -1 )
So half tau is the magnitude of the imaginary part of the natural logarithm of -1:
τ/2 = ln( -1 )/i